教学案例一：数学文化与存在性定理

存在性定理是大学数学学习中很重要的一类定理，但因为只是存在，而不知道具体是多少、在哪里，很多学生感觉不到其重要性。除了存在性定理，在数学的很多地方都需要存在性来保证运算或者论证的正确性。存在性的重要性与其中蕴含的数学文化是这次教学的重点。

在这里我们通过通俗的例子，数学文化的融入等教学手段，让学生体会、理解存在性的重要性。

1.向学生提问：请找出最大的素数（质数）。素数的概念中学都应该知道，学生可能会思考一会儿，感觉一时无法找到。由此引出问题：最大的素数是否存在？存在，才有找的意义；如果不存在，就是有天大的本事，也无济于事。教师可以借此机会展示一下用反证法证明最大素数不存在（素数有无限多个）。

所以，存在性的重要性可见一斑。

 

2. 给出微积分中第一个学习的存在性定理：介值性定理，理解存在性的价值，体会数学思想。

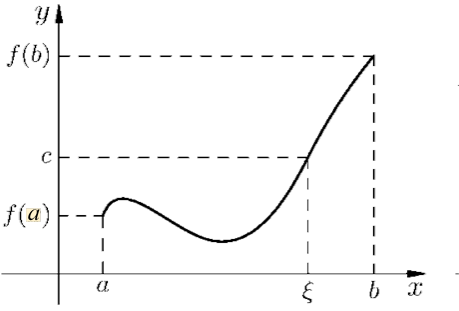介值性定理 设函数在闭区间上连续，且（不妨设），则对于任何一个介于与之间的实数： ，必定存在一点，使得。

 

定理可用上图加以解释：连续函数与直线（ ）一定存在交点（可能还不止一点，上图红色虚线），即，但具体是哪一点，却无法确定。

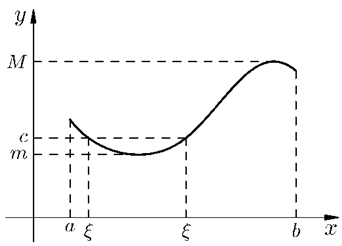介值性定理还可以做一个拓展（见图），端点的函数值可以用函数在闭区间上的最大值和最小值代替。

 

与介值性定理同时出现的还有连续函数的最大值与最小值定理，也是一个存在性定理，叙述如下。

最大、最小值定理 如果在闭区间上连续，则至少存在两个点，使得对所有的，有

。

这里和分别是在上的最小值和最大值，即的函数值在处取到最大值，在处取到最小值，但究竟和在哪里，定理没有说，一时也无法判定。

两个定理都只知道存在，不知道具体位置，但其在数学理论和应用中的重要性在下面的例子和今后的学习中将越来越清晰地展现在我们面前。

这种“存在性”问题在中学数学也遇见过，如抽屉原理：M个苹果放在N个抽屉里（M>N），那么一定存在一个抽屉，其中至少有两个苹果，但具体是哪一个抽屉，无法确定。

还有著名的代数学基本定理：任何一个n次代数方程在复数域上一定有n个根。定理只说存在n个根，但根在哪里，却没有说。

其他科学领域也有同样的情况。有些科学论断，确定某事物和某现象的存在，却不能指出存在的地方，或者说出具体的原因。但是，这些论断仍然具有重要的科学价值。例如：

对某个疾病，根据临床实验，知道几种药物服用后肯定有效，但是哪一种最有效，还说不清楚；通过野外调查，肯定东北大兴安岭某区域有野生东北虎存在，但是具体在哪里，还不能肯定。

 

3.存在性定理的人文意境。

唐朝诗人贾岛（779-843年，唐朝诗人）的有一首

《寻隐者不遇》的诗：

“松下问童子，言师采药去；

只在此山中，云深不知处”。

贾岛并非数学家，但是细细品味，觉得其诗的意境，简直是为数学而作，在人文意境上对存在性定理做了非常生动的描述：

老药师在哪里？他就在山中，但具体在山中的哪里，却不知道了。尽管没有马上见到老药师，但老药师没走远去采药了，有希望等老药师回来再发挥作用！

通过贾岛的诗把数学文化、人文意境融入进了存在性定理的教学。

 

4.很多时候存在是关键。比如刚才的找素数，又比如高中课本中的“二分法求根”的内容，就是通过科学计算器用“二分法”找出方程的根。不论用什么先进的计算器，关键是根要存在，才能找到，存在性定理起了关键的作用！

存在性问题，还存在于各类运算中。比如极限运算法则，两个函数相乘（相加，相除也一样）的极限等于两个函数极限的相乘，但如果有一个函数的极限不存在呢？显然两个函数的极限都要存在是前提。

中小学数学中还有其他的存在性问题，请学生自行举例。