教学案例二：问题驱动的拉格朗日中值定理

拉格朗日中值定理是微分学中非常著名的定理，主要是两点，一是应用定理可以讨论函数的单调性，极值，由此可以解决很多实际问题（最值问题）；二是定理本身蕴含的数学思想非常深刻，体现了局部与整体的关系。

本次教学的重点有两个，第一，通过问题驱动，让学生自己“发现”拉格朗日中值定理；第二，拉格朗日中值定理蕴含的数学思想。

教学过程是这样设计的：先不给出定理，而是问一系列的问题，由学生通过问题的思考和解答，自己“发现”拉格朗日中值定理。

重点一，“发现”定理。问题：平均速度和瞬时速度有关系吗？

这些概念在引入导数时都已经接触过，而且速度是非常生活化的，一定会引起学生的兴趣。

当然教师可以给出具体的数据：一汽车从高速公路的A口驶入高速公路，在距离A口50千米的B口下高速公路，总共用时40分钟。为了使问题更加简单直接，有利于引导学生的思路，可以把上面的问题分解成下面三个问题。

第一个问题：汽车在这段高速公路上行驶的平均速度是多少？ 学生会很快得出结果平均速度

千米/小时。

　

这时学生的思维已经调动起来了，马上可以问

第二个问题：在高速公路行驶时，汽车是否会始终以每小时75千米的速度行驶？

当然不会，肯定有时比每小时75千米慢，有时比每小时75千米快。学生应该会这样肯定地回答。这里的速度是指汽车的瞬时速度吗？也应该得到肯定地回答。

第三个问题（关键问题）：是否会有某个时刻，汽车行驶的瞬时速度恰好等于每小时75千米的平均速度？

有了前面问题的铺垫，学生通过思考，应该会给出肯定的答案。

于是，教师根据上面的问题，可以把问题规范成数学化的论述：一个物体的做直线运动，其位移函数为，物体在时间区间上的平均速度是否会与物体在这一时间段内某时刻的瞬时速度相等？即，是否存在，使得

？

我们只要假定速度是连续变化的，根据常识和连续函数的介值性定理，不难得出肯定的结论。（用到了上一案例的存在性定理，存在性在这里是多么的重要！）而结论的数学表示就是拉格朗日中值定理（公式）！

这样学生就“发现”了拉格朗日中值定理，这肯定会激发学生学习数学的兴趣，享受发现的快乐。

2.拉格朗日定理蕴含的数学思想。

现在可以完整规范地把拉格朗日中值定理叙述一下，并给出几何解释（发现过程是定理的物理解释）。

拉格朗日中值定理 如果函数在闭区间上连续, 在开区间上可导, 则至少存在一点, 使得

        （1）

或

      （2）

 

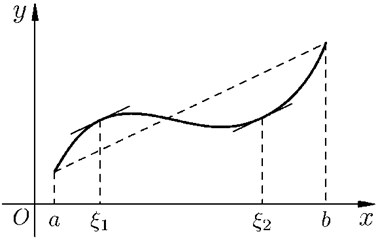
这个公式称为拉格朗日公式，它的几何解释见图，即在曲线上至少有一点的斜率等于曲线两个端点连线的斜率。

然后对公式进行深入分析。首先请学生分析公式两边式子所表达的意义，教师最后进行总结：公式左边是导函数在一点的值（尽管还不知道这点在哪里），是一种局部性质；而右边则是函数在区间上的增量，是一种整体性质，得出公式两边串联起了导函数的局部性质和函数的整体性质，这样两个看似并不相关的数学概念，通过拉格朗日公式（1）或（2）就联系起来了，如果知道了导数的每一点某种性质就可以得到函数在区间上的一种整体性质。比如，如果导数在区间上处处大于零，那么一定有。

最后有两点解释。第一，公式（1）右边表达的是一种平均值，因此中值定理也是“平均值定理”。第二，中值定理就像就像一座大桥，把大河两岸（不相关）的两个重要景点（数学概念）联通了，借用一句毛主席诗词，就是“一桥飞架南北，天堑变通途”！中值定理使得导数大大拓展了应用范围，可以用导数解决函数的单调性和极值（最值），建立求不定时极限的洛必达法则等等。