

(原载《数学教学》2009年第2期)
13世纪意大利数学家莱昂纳多·斐波那契(Leonardo Fibonacci)在他所著的《算盘全集》中提出一个有趣的兔子问题. 他说: 有一对小兔, 若第二个月它们成年, 第三个月开始每一个月都生下一对小兔, 而所生小兔亦在第二个月成年, 第三个月开始也每个月生下一对小兔(这里假定每个月所生下的一对小兔必为一雌一雄, 且均无死亡), 试问一年后共有小兔几对? 为此, 我们不妨计算一下每个月底兔子对的数目, 它们依次是:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
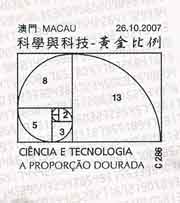
也就是说在一年末了时兔子对的数目是144对. 邮票图1中列举了2, 3, 4, 5, 6, 7月底小兔的对数. 这些数目的规律是: 设un为第n个月兔子对的数目, 于是u1=u2=1, un+1=un-1+un (n>1). 当n取遍自然数时得到数列{un}称为斐波那契数列. 数列中的数称为斐波那契数. 由于limn→∞ un/un+1=(√5-1)/2(黄金分割数), 故斐波那契数与黄金分割有着密切的联系. 它们可以作如下的几何解释: 若依次作边长为1, 1, 2, 3, 5, 8, 13(斐波那契数)等的正方形, 按图2(纪念邮戳)拼接成矩形, 那么这个矩形就将无限地趋近于黄金矩形(即矩形的短边与长边之比等于黄金分割数). 再进一步, 若对每个正方形都以边长为半径作一段内接圆弧, 按图2连接起来, 就得到鹦鹉螺线. 邮票图3给出了鹦鹉螺的剖面图.
图 1(左); 图 2(中); 图 3(右)
斐波那契数列并不只是数学家们的臆造, 已经发现很多自然现象符合斐波那契数规律. 特别在植物世界中, 几乎所有花卉的花瓣基数是斐波那契数. 如菊花是2基数; 兰花和鹤望兰都是3基数; 梅花、凤凰木和扶桑等是5基数. 我们都知道松树的针叶数, 只有两针松(图4, 前苏联邮资信封), 三针松(图5, 马拉维邮票)和五针松(图6, 保加利亚邮票), 没有四针松. 观察向日葵的花盘, 可发现其种子排列是正反两个方向相嵌在一起的螺旋线(图7), 而螺旋线的数目, 一般是34和55、55和89或89和144, 这每组数字都是斐波那契数列中相邻的两个数. 此外, 在植物的叶子、枝条、果实、种子等形态特征上都可发现斐波那契数的存在. 上述图1、3、7是澳门《黄金比例》这一套邮票中的3枚邮票.
图 4
图 5(左); 图 6(中); 图 7(右)
斐波那契数列的应用还很多, 美国的《斐波那契季刊》专门刊登这方面新发现的应用和理论. 由此可见, 斐波那契数列被人们关注的程度.
(点击邮票小图可以显示更清晰大图)