(原载《数学教学》2009年第1期)
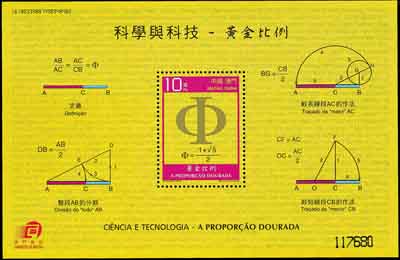
2007年10月26日澳门发行了“科学与技术 — 黄金比例”的一套邮票, 它包含一枚小型张(图1)和四枚邮票(图2, 另3枚另文介绍). 所谓黄金分割(或黄金比例)是说: 若点C将线段AB外分或内分为两部AC和BC, 使AC2=AB·BC, 这样的分割称为黄金分割. 如果将上述等式改写成AB/AC=AC/BC, 则称它为黄金比例(见图1四周各图). 如果设AB=a, 当C外分线段AB时, 可求得AC=(1+√5)/2a, 无理数(1+√5)/2常用Φ表示(见图1中间的邮票, 此小型张背景图则列出数值Φ小数点后4374位数字, 本套邮票的其他各枚也有同样的背景), 常用的近似值为1.618. 若C是内分线段AB, 则有AC=a/Φ. 1/Φ的常用近似值是0.618, 称为黄金分割数(或黄金数). 线段的这种分割从古希腊开始就被人们视作“贵比黄金”, 这就是黄金分割名称的由来.
图 1
五角星与彭罗斯镶嵌 构成正五角星的每一个角都是顶角为36°的等腰三角形, 它的底边与腰的比正好等于黄金分割数. 1974年英国数学物理学家罗杰·彭罗斯(Roger Penrose, 1931-)设计出一种地砖图案, 它只含有两个不同形状的具有黄金分割特性的四边形(见图2的放大图), 用这两种特殊四边形就能无缝隙地铺满整个地面(图2).
图 2
黄金分割的应用 黄金分割除了上述提到的应用之外, 还用于优选法中选优过程, 称为黄金分割法(图3为中国极限明信片, 片图是华罗庚先生在介绍如何在优选法中应用黄金分割法选优). 黄金分割还用于绘画、 建筑设计等等. 人们认为当这些艺术品中的比例符合黄金分割时, 最和谐、最漂亮. 例如古埃及金字塔(图4)的高与底边的比就近似于黄金分割数. 当然黄金分割的应用还有多, 限于篇幅这里就不一一列举了.
图 3(左); 图 4(右)
(点击邮票小图可以显示更清晰大图)